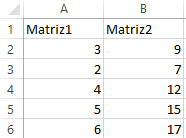
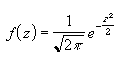Excel es un programa informático desarrollado por la empresa Microsoft y forma parte de la suite ofimática desarrollada principalmente para el entorno de Windows. Excel es una hoja de cálculo que permite trabajar con datos
numéricos, con los cuales se pueden realizar cálculos aritméticos básicos o aplicar funciones matemáticas de mayor complejidad estadística. Para este caso en particular se describirán algunas de las herramientas con las que
cuenta Excel para llevar a cabo un análisis estadístico.
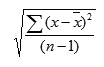

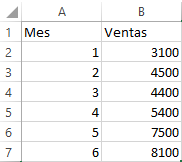
Se calcula la estimación de las ventas en el noveno mes, basándose en las ventas de los meses 1 al 6.